Entendendo a Teoria dos Conjuntos através da Vida Cotidiana

A Teoria dos Conjuntos é um ramo da matemática que estuda conjuntos, que são coleções de objetos. Esses objetos podem ser qualquer coisa: números, pessoas, letras, ideias, entre outros. No centro deste estudo, está a ideia de agrupar, classificar e relacionar diferentes coleções, baseando-se em características ou propriedades comuns.
Mas por que seria importante entender essa teoria? Em primeiro lugar, ela serve como base para quase todos os outros ramos da matemática e é frequentemente aplicada em lógica, estatística, probabilidade e até mesmo na ciência da computação. Porém, além da sua importância acadêmica, a Teoria dos Conjuntos possui uma aplicação prática e visível em nosso cotidiano. Todos os dias, sem que muitas vezes percebamos, classificamos, agrupamos e organizamos informações e objetos baseados em características comuns. Seja ao separar os legumes das frutas em nossa lista de compras, ao dividir nossos contatos telefônicos por categorias profissionais ou pessoais, ou ao agrupar músicas por gêneros em nossas playlists, estamos, intuitivamente, utilizando princípios da Teoria dos Conjuntos.
Ao longo deste artigo, exploraremos como essa teoria, muitas vezes vista como uma abstração matemática, está, na verdade, profundamente enraizada em nossas atividades diárias e na maneira como compreendemos e interagimos com o mundo à nossa volta.
1. O Básico da Teoria dos Conjuntos:
Definição de Conjunto:
Um conjunto é uma coleção de objetos bem definidos, considerados como uma entidade única. Estes objetos são chamados de elementos do conjunto. A particularidade da Teoria dos Conjuntos é que ela trata os conjuntos como objetos em si, independentemente da natureza ou características dos seus elementos. Por exemplo, o conjunto de todos os números ímpares menores que 10 é {1, 3, 5, 7, 9}.
Elementos de um Conjunto:
Os objetos que fazem parte de um conjunto são denominados elementos. Eles podem ser qualquer coisa: números, letras, objetos físicos, entre outros. Usamos a notação a ∈ A para indicar que “a” é um elemento do conjunto A. Inversamente, se “b” não pertence ao conjunto A, escrevemos b ∉ A. Por exemplo, considerando o conjunto B = {2, 4, 6, 8}, podemos afirmar que 4 ∈ B e 3 ∉ B.
Tipos de Conjuntos:
Os conjuntos podem ser classificados de diferentes maneiras, dependendo do número ou da natureza de seus elementos:
Conjunto Finito:
É aquele que possui um número contável e limitado de elementos. Por exemplo, o conjunto C = {a, b, c, d} é finito porque contém exatamente quatro elementos.
Conjunto Infinito:
Possui uma quantidade ilimitada de elementos. Um exemplo clássico é o conjunto dos números naturais, N, que inclui {0, 1, 2, 3, …} e assim por diante, indefinidamente.
Conjunto Vazio:
Também conhecido como conjunto nulo, é o conjunto que não possui nenhum elemento. Representado pelo símbolo Ø, é importante notar que o conjunto vazio é subconjunto de qualquer conjunto.
Além desses, existem muitos outros tipos de conjuntos, como conjuntos unitários, conjuntos universais, entre outros, que são definidos com base em diferentes critérios ou contextos. O importante é entender que, através da classificação e agrupamento, a Teoria dos Conjuntos nos oferece ferramentas para organizar e compreender o mundo ao nosso redor de forma sistemática. A identificação e organização de conjuntos em nossa vida cotidiana, muitas vezes feita de forma intuitiva, evidenciam a presença e aplicação da Teoria dos Conjuntos em ações práticas do dia a dia. Essas organizações nos ajudam a criar uma estrutura, otimizar nossas atividades e tornar nossas decisões mais informadas e sistemáticas. Ao compreendermos a lógica subjacente dessas ações cotidianas, torna-se evidente a relevância e aplicabilidade da Teoria dos Conjuntos em diversas facetas de nossas vidas.
2. Operações com Conjuntos no Cotidiano:
União:
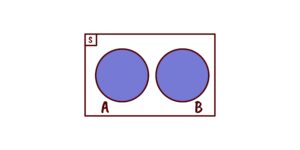
Imagine que você está planejando uma festa e deseja atender às necessidades alimentares de todos os convidados. Se temos dois grupos distintos, um de vegetarianos e outro de onívoros, ao elaborar um cardápio que atenda a ambos, estamos fazendo a união desses dois conjuntos. Por exemplo, um cardápio que inclua tanto opções vegetarianas (saladas, legumes, massas) quanto carnes e peixes. A união nos permite combinar elementos de diferentes conjuntos para criar um conjunto mais abrangente, garantindo que nenhuma preferência seja deixada de fora.
Intersecção:
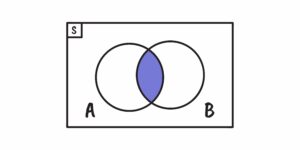
As redes sociais tornaram-se uma parte integral de nossas vidas. Quando visitamos o perfil de um amigo e vemos os “amigos em comum”, estamos observando a intersecção entre o nosso conjunto de amigos e o conjunto de amigos daquela pessoa. Esta intersecção nos mostra as conexões compartilhadas e pode ser uma ferramenta valiosa para estreitar relações ou reacender amizades.
Diferença:
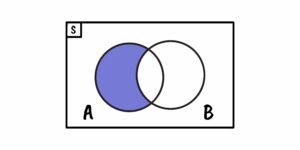
Todos nós temos gostos musicais únicos. Ao comparar sua playlist de música atual com a de um amigo, as músicas que você tem e ele não tem representam a diferença entre os dois conjuntos. Isso pode ser uma forma divertida de descobrir novas músicas ou redescobrir faixas que havíamos esquecido.
Complemento:
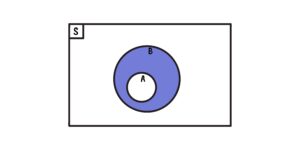
Ao longo de nossos dias, muitas vezes temos listas de tarefas a cumprir. Se marcamos algumas tarefas como “realizadas” e outras não, o conjunto de tarefas “ainda não realizadas” é o complemento do conjunto de tarefas “realizadas”. Identificar o complemento nos ajuda a focar no que ainda precisa ser feito e a priorizar nosso tempo de maneira eficaz.
Estas operações com conjuntos, que muitas vezes realizamos de forma intuitiva em nosso cotidiano, nos ajudam a organizar informações, tomar decisões e entender relações entre diferentes grupos ou categorias.
3. Diagramas de Venn e sua Representação Visual:

Os Diagramas de Venn são representações gráficas que utilizam círculos ou outras formas para ilustrar as relações entre dois ou mais conjuntos. Cada círculo representa um conjunto, e as áreas onde os círculos se sobrepõem representam a intersecção entre os conjuntos, ou seja, os elementos que pertencem a ambos. Esses diagramas foram criados pelo matemático e filósofo John Venn no final do século XIX, mas sua aplicação transcende a matemática, sendo útil em diversas áreas do conhecimento e situações do dia a dia.
Como eles podem ser usados para visualizar relacionamentos em situações cotidianas:
Imagine que você e dois amigos estão discutindo suas bandas favoritas. Cada um de vocês tem uma lista de bandas que gosta. Ao representar essas listas em um Diagrama de Venn com três círculos, as áreas de sobreposição mostrarão quais bandas são apreciadas por mais de uma pessoa. Por exemplo, o ponto onde os três círculos se encontram pode revelar uma banda que todos vocês gostam, enquanto as áreas onde apenas dois círculos se sobrepõem mostrarão as bandas que dois de vocês gostam. As áreas sem sobreposição mostrarão as bandas que são preferidas exclusivamente por uma pessoa.
Além das preferências musicais, os Diagramas de Venn podem ser utilizados em diversas situações do nosso cotidiano:
Alimentação:
Se estiver planejando um jantar para amigos com diferentes restrições alimentares (por exemplo, veganos, vegetarianos e onívoros), um Diagrama de Venn pode ajudar a visualizar quais pratos atenderão a todos e quais são específicos para determinados grupos.
Hobbies:
Ao tentar organizar um fim de semana entre amigos, pode-se usar o diagrama para encontrar atividades que todos gostam, ou aquelas que apenas alguns gostam, facilitando o planejamento.
Estudos:
Em um grupo de estudos, um Diagrama de Venn pode mostrar quais tópicos todos os estudantes já dominam, quais precisam ser revisados por alguns, e quais são desconhecidos pela maioria.
Os Diagramas de Venn, com sua representação visual clara e intuitiva, são ferramentas valiosas que nos ajudam a entender, de forma rápida, as relações entre diferentes conjuntos e a tomar decisões informadas em diversas situações da vida diária.
4. Aplicações Avançadas da Teoria dos Conjuntos:
A Teoria dos Conjuntos, embora possa parecer uma abordagem simplista da matemática à primeira vista, encontra aplicações profundas e amplas em diversos campos avançados do conhecimento.
Lógica:
A lógica matemática frequentemente utiliza a Teoria dos Conjuntos como base para desenvolver proposições, argumentos e validações. Conjuntos são empregados para descrever domínios de discursos, estabelecendo assim a estrutura para argumentos lógicos e o desenvolvimento de teoremas.
Probabilidade:
No campo da probabilidade, o espaço amostral de um experimento aleatório é frequentemente representado como um conjunto, e os eventos (resultados de interesse) são subconjuntos desse espaço. A operação de união, intersecção e complemento entre conjuntos desempenha um papel crucial na determinação de probabilidades combinadas e condicionais.
Estatística:
Conjuntos são fundamentais na categorização de dados. Ao analisar grandes volumes de informações, frequentemente agrupamos dados em conjuntos ou subconjuntos para realizar análises estatísticas, como medidas de tendência central ou dispersão.
Ciência da Computação:
A teoria dos conjuntos é intrínseca à ciência da computação, especialmente em áreas como teoria dos autômatos, teoria dos grafos e bancos de dados. Algoritmos que trabalham com bancos de dados, por exemplo, frequentemente operam em conjuntos de informações.
Conjuntos Infinitos e o “Hotel de Hilbert”:

Um dos conceitos mais intrigantes da Teoria dos Conjuntos é a ideia de conjuntos infinitos. O “Hotel de Hilbert”, uma analogia concebida pelo matemático David Hilbert, descreve um hotel com infinitos quartos, todos ocupados. Surpreendentemente, mesmo estando completamente ocupado, o hotel pode sempre acomodar mais hóspedes, simplesmente movendo cada hóspede para o quarto com número seguinte ao seu. Essa analogia ilustra propriedades paradoxais, mas matematicamente consistentes, dos conjuntos infinitos e da natureza do infinito em si.
Essas aplicações mostram que a Teoria dos Conjuntos não é apenas uma ferramenta didática, mas uma área robusta da matemática que tem implicações profundas em muitos campos avançados do conhecimento.
Conclusão:
A Teoria dos Conjuntos, em sua essência, é um ramo da matemática que se debruça sobre o estudo de coleções de objetos, sejam eles simples ou complexos. No entanto, sua abrangência vai muito além de simples definições ou diagramas. Como vimos, sua aplicabilidade se estende desde tarefas diárias cotidianas até conceitos mais avançados e especializados em diferentes disciplinas.
Tal teoria nos permite organizar, categorizar e visualizar elementos, grupos e suas relações de maneira clara e lógica. Além disso, oferece ferramentas poderosas para resolver problemas, entender fenômenos e elaborar raciocínios matemáticos mais aprofundados.
Por fim, para aqueles que buscam uma representação visual e sintetizada deste vasto e fascinante tópico num nível introdutório, recomendo fortemente o “Resumo Gráfico sobre Conjuntos”. Este recurso ilustra de forma concisa os conceitos fundamentais, facilitando a compreensão e servindo como um guia prático para estudantes e entusiastas.
Disponível aqui: “Resumo Gráfico sobre Conjuntos”
Quer aprofundar seu entendimento sobre a matemática e ver como ela se aplica em mais aspectos da sua vida?
Descubra o método que está transformando estudantes em verdadeiros mestres da matemática! Clique aqui para acessar o e-book “Néctar Supremo da Matemática” de Sandro Curió e comece a sua jornada rumo ao sucesso agora mesmo! Acesse agora!
Você pode tirar um notão em Matemática este ano seguindo o passo a passo desse E-book




