Função Exponencial: Um Guia Completo com Mapa Mental

As funções exponenciais são fundamentais em diversas áreas da matemática e suas aplicações se estendem a campos como a economia, biologia, física e engenharia. Neste artigo, apresentaremos um resumo completo sobre a função exponencial, acompanhando um mapa mental para facilitar a compreensão e o estudo.

O que é uma Função Exponencial?

Uma função exponencial é uma função da forma
𝑓(𝑥)=𝑎⋅𝑏^𝑥, onde:

• 𝑎 é uma constante não nula,
• b é uma base positiva diferente de 1,
• 𝑥 é a variável independente.

Propriedades das Funções Exponenciais

As principais propriedades das funções exponenciais incluem:

• Crescimento e Decrescimento: Dependendo do valor da base b, a função pode representar um crescimento exponencial (se 𝑏>1) ou um decrescimento exponencial (se 0<b<1).
• Assíntota Horizontal: As funções exponenciais possuem uma assíntota horizontal no eixo y=0.
• Continuidade e Diferenciabilidade: As funções exponenciais são contínuas e diferenciáveis em todo o seu domínio.

Gráficos das Funções Exponenciais

Os gráficos das funções exponenciais variam conforme os valores dos parâmetros 𝑎 e 𝑏. Exemplos típicos incluem:

• 𝑓(𝑥) = 2^𝑥: exemplo de crescimento exponencial.
• 𝑓(𝑥) = (1/2)^𝑥: exemplo de decrescimento exponencial.

Aplicações das Funções Exponenciais

As funções exponenciais são amplamente utilizadas em diversas áreas:

• Economia: Modelagem de crescimento populacional, inflação, juros compostos.
• Biologia: Crescimento de populações, decaimento radioativo.
• Física: Leis de decaimento exponencial, como a lei de resfriamento de Newton.
• Engenharia: Análise de circuitos elétricos, processos de controle.

Exemplo Prático

Vamos considerar um exemplo prático para ilustrar o uso de funções exponenciais:

Problema: Suponha que uma população de bactérias dobra a cada hora. Se inicialmente há 100 bactérias, quantas bactérias haverá após 5 horas?

Solução: Usamos a função exponencial
𝑃(𝑡) = 𝑃₀⋅2^𝑡, onde 𝑃₀ = 100 e 𝑡 é o tempo em horas.
𝑃(5) =100⋅2⁵ = 100⋅32 = 3200
Portanto, haverá 3200 bactérias após 5 horas.

Quer ser aprovado esse ano, mas não sabe por qual caminho seguir? Eu tenho a solução.

Você pode tirar um notão em Matemática em 2024seguindo o passo a passo desse E-book.

Chega de travar nas questões de Matemática e se desesperar na prova.
Tenha acesso as principais dicas comprovadas para conseguir a tão sonhada aprovação nesse ano!

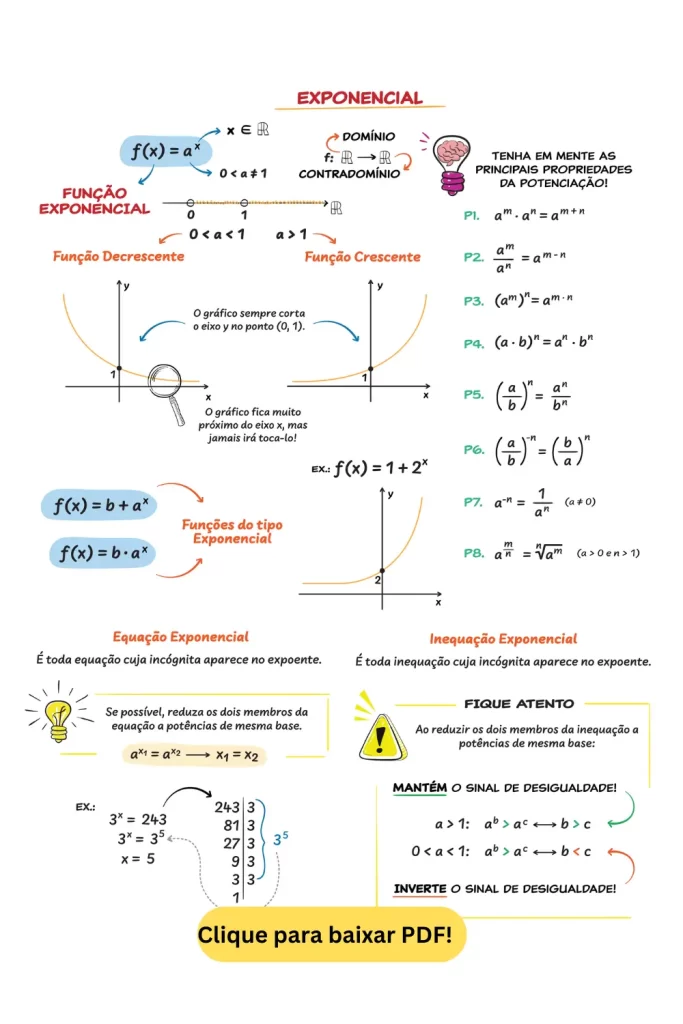
Mapa Mental da Função Exponencial

Para facilitar o estudo, preparamos um mapa mental que resume os principais pontos sobre as funções exponenciais. Clique aqui para baixar o PDF.

Conclusão

Compreender as funções exponenciais é essencial para o estudo de diversas disciplinas científicas. Esperamos que este resumo, juntamente com o mapa mental, ajude a consolidar seu entendimento sobre o assunto.

 

---