Função Quadrática: Um Guia Completo com Mapa Mental

A função quadrática é um tópico essencial em álgebra e aparece frequentemente em diversas áreas da matemática. Neste artigo, apresentaremos um resumo completo sobre a função quadrática, acompanhando um resumo gráfico (“mapa mental”) detalhado para facilitar a compreensão e o estudo.

O que é uma Função Quadrática?

Uma função quadrática é uma função polinomial de segundo grau da forma

$f(x) = ax^2 + bx + c$ , onde:

• $a$  é o coeficiente quadrático ( $a \neq 0$  ),
• $b$  é o coeficiente linear,
• $c$  é o coeficiente constante,
• $x$  é a variável independente.

Propriedades das Funções Quadráticas

As principais propriedades das funções quadráticas incluem:

• Forma do Gráfico: O gráfico de uma função quadrática é uma parábola.
• Concavidade: A parábola pode ser côncava para cima (se $a > 0$  ) ou para baixo (se $a < 0$  ).
• Vértice: O vértice da parábola é o ponto onde ela muda de direção,
• Eixo de Simetria: O eixo de simetria é a linha vertical que passa pelo vértice, dada pela equação $x = -\frac{b}{2a}$  .

Zeros da Função Quadrática

Os zeros ou raízes da função quadrática são os valores de

$x$ para os quais $f(x) = 0$ . Eles podem ser encontrados usando a fórmula quadrática: $x = \frac{-b \pm \sqrt{b^2 – 4ac}}{2a}$

Aplicações das Funções Quadráticas

As funções quadráticas têm diversas aplicações práticas, incluindo:

• Física: Modelagem de trajetórias de projéteis.
• Economia: Análise de custos e receitas.
• Engenharia: Otimização de processos.
• Geometria: Cálculo de áreas e volumes.

Exemplo Prático

Vamos considerar um exemplo prático para ilustrar o uso de funções quadráticas:

Problema: Uma bola é lançada de uma altura de 1,5 metros com uma velocidade inicial de 10 m/s. Sua altura

$h$ em metros, após $t$ segundos, é dada por: $h(t) = -4,9t^2 + 10t + 1,5$  

Solução: Para encontrar o tempo em que a bola atinge a altura máxima, usamos o vértice da parábola:

$t = -\frac{10}{2 \cdot -4,9} = \frac{10}{9,8} \approx 1,02 \, \text{segundos}$  

A altura máxima é:

$h(1,02) = -4,9(1,02)^2 + 10(1,02) + 1,5 \approx 6,6 \, \text{metros}$  

Quer ser aprovado esse ano, mas não sabe por qual caminho seguir? Eu tenho a solução.

Você pode tirar um notão em Matemática em 2025 seguindo o passo a passo desse E-book.

Chega de travar nas questões de  Matemática e se desesperar na prova. Tenha acesso as principais dicas comprovadas para conseguir a tão sonhada aprovação nesse ano!

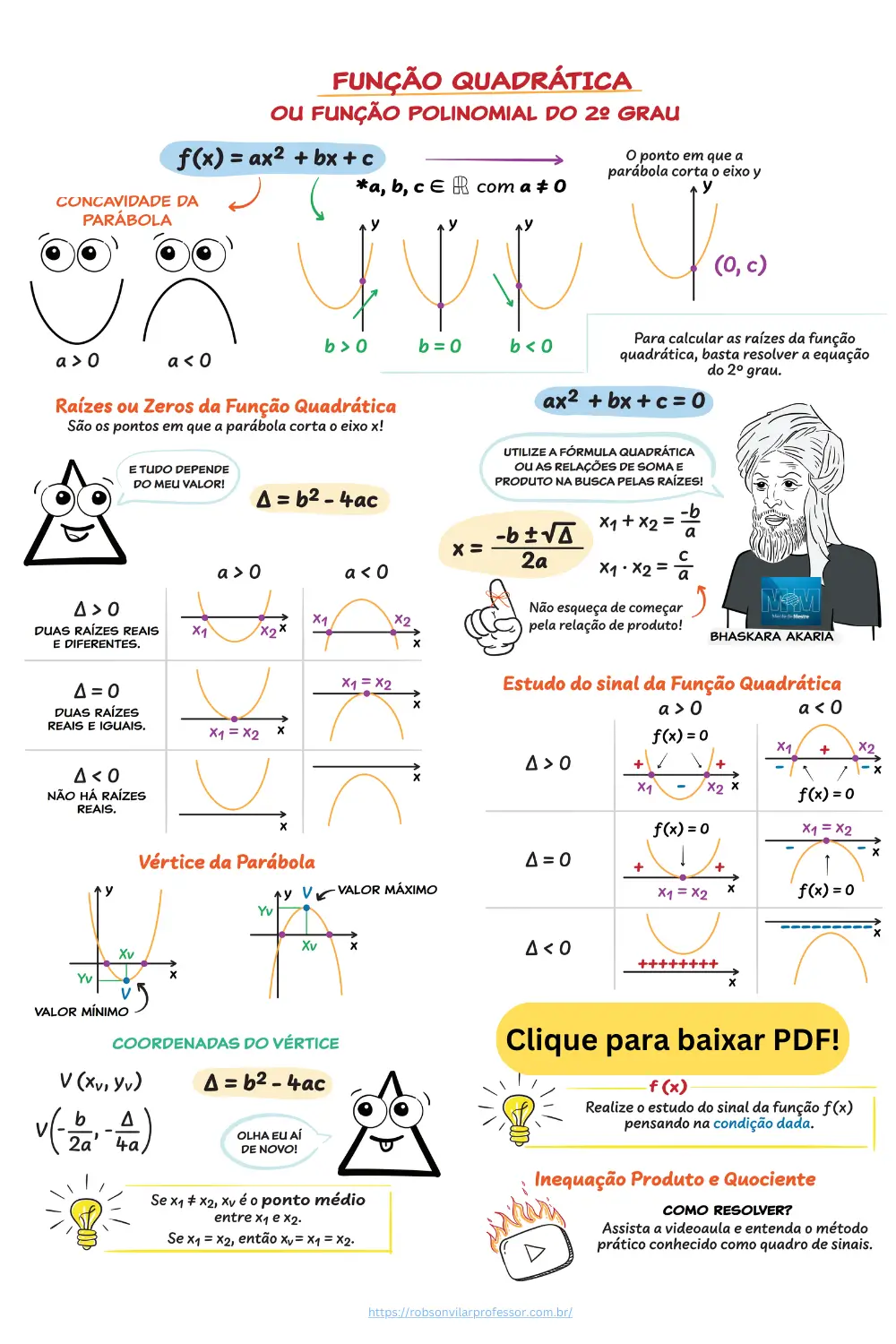
Mapa Mental da Função Quadrática

Para facilitar o estudo, preparamos um mapa mental que resume os principais pontos sobre as funções quadráticas. Clique aqui para baixar o PDF.

Conclusão

Compreender as funções quadráticas é crucial para o estudo de álgebra e suas aplicações em diversas disciplinas. Esperamos que este resumo, juntamente com o mapa mental, ajude a consolidar seu entendimento sobre o assunto.

Pronto para dominar a matemática e arrasar nos exames?

Descubra o método que está transformando estudantes em verdadeiros mestres da matemática! Clique aqui para acessar o e-book “Néctar Supremo da Matemática” de Sandro Curió e comece a sua jornada rumo ao sucesso agora mesmo! Acesse agora!

Você pode tirar um notão em Matemática este ano seguindo o passo a passo desse E-book

---