Simulado de Matemática para o 9º Ano – Questões por Descritor

A preparação para avaliações nacionais é fundamental no ensino fundamental, e o 9º ano é um momento crítico para solidificar conceitos matemáticos essenciais. Este artigo propõe um simulado de matemática baseado em descritores específicos que refletem as habilidades exigidas pelo MEC em provas como o Saeb e a Prova Brasil.
Estrutura do Simulado
O simulado é organizado por descritores, que detalham habilidades matemáticas específicas que os alunos devem dominar ao final do ensino fundamental. Cada descritor é acompanhado por questões modeladas para avaliar essas habilidades em um contexto prático e teórico.
Como Usar o Simulado
- Revisão dos Descritores: Antes de iniciar o simulado, é recomendável que professores revisem os descritores com os alunos, explicando cada competência matemática relacionada.
- Resolução das Questões: Os alunos devem tentar resolver as questões individualmente para simular uma situação de prova real.
- Discussão em Grupo: Após a tentativa individual, é útil discutir as questões em grupo para esclarecer dúvidas e consolidar o aprendizado.
Benefícios do Simulado
Utilizar questões por descritor ajuda os alunos a entenderem melhor onde precisam focar seus estudos e como os conceitos matemáticos são aplicados em diferentes contextos. Além disso, prepara os estudantes para o formato e o nível de dificuldade das avaliações oficiais, aumentando sua confiança e competência.
Este simulado é uma ferramenta valiosa para educadores que buscam preparar seus alunos de maneira eficaz para as avaliações nacionais, garantindo que eles não apenas compreendam a matéria, mas também sejam capazes de aplicá-la em diversos contextos.
Simulado
Eixo do Conhecimento: Números.
Eixo Cognitivo: Compreender e aplicar conceitos e procedimentos.
Cód. Habilidade: 9N1.1 – Escrever números racionais (representação fracionária ou decimal finita) em sua representação por algarismos ou em língua materna OU associar o registro numérico ao registro em língua materna.
Questões:
1. (PAEBES) No desenho abaixo está representado o medidor de combustível de um carro.
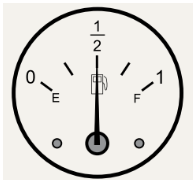
Qual é a representação decimal do número que o ponteiro desse medidor de combustível está indicando?
A) 0,5
B) 1,2
C) 2,0
D) 2,1
2. (SAEP 2013) Abner comprou uma barra de chocolate e dividiu em dez partes iguais, das quais comeu duas, como mostrado na figura abaixo.
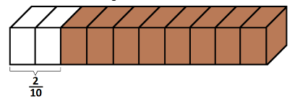
Outra forma que podemos representar a parte que Abner comeu da barra de chocolate é
(A) 0,2.
(B) 0,02.
(C) 0,8.
(D) 0,08.
3. (SAE-GO) O quadrado abaixo foi dividido em 8 partes iguais.
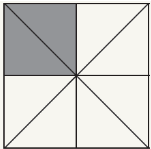
Em relação a parte destacada de cinza, uma representação correta dessa fração é:
A) dois sextos.
B) dois oitavos.
C) seis dois.
D) seis oitavos.
Eixo do Conhecimento: Números.
Eixo Cognitivo: Compreender e aplicar conceitos e procedimentos.
Cód. Habilidade: 9N1.2 – Compor OU decompor números racionais positivos (representação decimal finita) na forma aditiva, ou em suas ordens, ou em adições e multiplicações.
Questões:
4. (Prova Brasil) O número decimal que é decomposto em
5 + 0,06 + 0,002 é
A) 5,62
B) 5,602
C) 5,206
D) 5,062
5. (SARESP) Qual é a resposta correta para a raiz quadrada de ![]() , com aproximação até centésimos?
, com aproximação até centésimos?
A) 4,7
B) 479
C) 4,79
D) 4,795
6. (SAERJ) Veja os números abaixo.
![]()
O algarismo 4 está ocupando a ordem dos milésimos no número
A) 1,48
B) 1,048
C) 1,0048
D) 1,00048
Eixo do Conhecimento: Números.
Eixo Cognitivo: Compreender e aplicar conceitos e procedimentos.
Cód. Habilidade: 9N1.3 -Identificar números racionais ou irracionais.
Questões:
7. (CEFAF) Observe as afirmativas:
(I) 3/4 é um número racional.
(II) 11/7 é um número irracional.
(III) 20/ 5 é um número natural.
(IV) 1/ 3 é um número inteiro.
São verdadeiras as afirmativas
A) (I) e (II).
B) (I) e (III).
C) (III) e (IV).
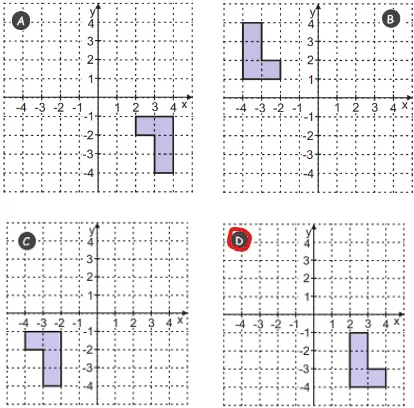
D) (II) e (III).
Eixo do Conhecimento: Números.
Eixo Cognitivo: Compreender e aplicar conceitos e procedimentos.
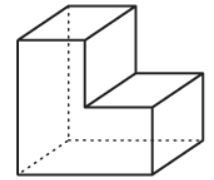
Cód. Habilidade: 9N1.4 – Comparar OU ordenar números reais, com ou sem suporte da reta numérica, OU aproximar números reais para múltiplos da potência de 10 mais próxima.
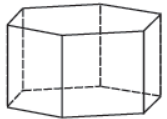
Questões:
8. (PAEBES) Observe abaixo a reta numérica em que os segmentos marcados estão igualmente espaçados.

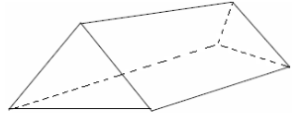
Nessa reta, os pontos que representam os números – 2 e 3 são, respectivamente,
A) P e Q.
B) Q e S.
C) R e S.
D) R e P.
9. (SPAECE) Veja a reta numérica abaixo.
![]()
Nessa reta, o ponto P corresponde ao número
A) 5
B) 4
C) -3
D) -6
Eixo do Conhecimento: Números.
Eixo Cognitivo: Compreender e aplicar conceitos e procedimentos.
Cód. Habilidade: 9N1.5 – Calcular o resultado de adições, subtrações, multiplicações ou divisões envolvendo números reais.
Questões:
10. (Prova Brasil) Fazendo-se as operações indicadas em 0,74 + 0,5 – 1,5 obtém-se:
A) – 0,64
B) – 0,26
C) 0,26
D) 0,64.
11. (PAEBES) Seja M = 0,03 + 1 + 2,5 + 3,004.
O valor de M é
A) 3,033
B) 3,159
C) 5,544
D) 6,534
12. (SAEP 2013) A pirâmide invertida abaixo foi construída da seguinte forma: cada número da linha abaixo é a soma dos números que estão imediatamente acima.

Seguindo o exemplo, descubra o número da letra F.
A) 10
B) -10
C) 2
D) – 4
Eixo do Conhecimento: Números.
Eixo Cognitivo: Compreender e aplicar conceitos e procedimentos.
Cód. Habilidade: 9N1.6 – Calcular o resultado de potenciação ou radiciação envolvendo números reais.
Questões:
13. (Saresp-2009) O número real ![]() está localizado no intervalo compreendido entre
está localizado no intervalo compreendido entre
A) 0 e 1.
B) 1 e 2.
C) 2 e 3.
D) 3 e 4.
14. (SAEGO 2013 – adaptado) Resolva a operação abaixo:
![]()
O resultado aproximado dessa operação é
A) 5
B) 7,07
C) 8,65
D) 10
Eixo do Conhecimento: Números.
Eixo Cognitivo: Compreender e aplicar conceitos e procedimentos.
Cód. Habilidade: 9N1.7 – Representar frações menores ou maiores que a unidade por meio de representações pictóricas OU associar frações a representações pictóricas.
Questões:
15. (PROEB) Veja, abaixo, o trapézio que foi dividido em 4 triângulos iguais.
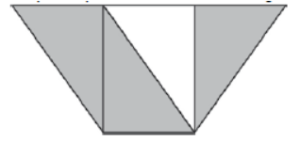
A região cinza corresponde a uma fração da área total do trapézio. Qual é essa fração?
A)![]()
B)![]()
C)![]()
D)![]()
16. (PROVA BRASIL) Rafael dividiu uma torta em oito pedaços iguais e comeu dois.
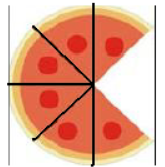
Que fração representa o pedaço que Rafael comeu?

Eixo do Conhecimento: Números.
Eixo Cognitivo: Compreender e aplicar conceitos e procedimentos.
Cód. Habilidade: 9N1.8 – Identificar frações equivalentes.
Questões:
17. (2ª P.D – 2013 – Seduc-GO) Observe as frações a seguir:
![]()
São equivalentes as frações
A) I e III.
B) I e IV.
C) II e III.
D) I, II, III e IV.
18. (Reforço digital – RJ) Observe o quadrinho abaixo e assinale a opção que conclui corretamente a discussão do casal.

A) Essa discussão é inútil, pois as quantias são iguais.
B) Ele está com a razão, pois ela quer muito mais dinheiro do que ele ofereceu.
B) Ela está com a razão, pois ele está oferecendo muito pouco dinheiro.
D) Essa discussão é inútil, pois ela está pedindo uma quantia inferior a que ele está oferecendo.
Eixo do Conhecimento: Números.
Eixo Cognitivo: Compreender e aplicar conceitos e procedimentos.
Cód. Habilidade: 9N1.9 – Converter uma representação de um número racional positivo paraoutra representação.
Questões:
19. (Prova Brasil) No Brasil, ![]() da população vive na zona urbana. De que outra forma podemos representar esta fração?
da população vive na zona urbana. De que outra forma podemos representar esta fração?
A) 15%
B) 25%
C) 34%
D) 75%
20. (SaeRJ) As florestas tropicais são o lugar do planeta onde a vida se manifesta com maior riqueza e intensidade. Nelas estão concentradas aproximadamente 70% das espécies vegetais e animais hoje existentes.
(Adaptado de Greenpeace. Florestas tropicais: Amazônia em perigo.Dados de 2005.)
A quantidade aproximada de espécies também pode se representada por
A) 7/1000 de espécies.
B) 7/100 de espécies.
C) 0,07 de espécies.
D) 0,70 de espécies.
Eixo do Conhecimento: Números.
Eixo Cognitivo: Compreender e aplicar conceitos e procedimentos.
Cód. Habilidade: 9N1.10 – Determinar uma fração geratriz para uma dízima periódica.
Questões:
21. (SUSEP – ESAF) Indique qual o número racional geratriz da dízima periódica 7,233…
A) 723/99
B) 723/90
C) 716/99
D) 651/90
22. (Brasil Escola) Analise a fração a seguir:
![]()
Podemos afirmar que ela é a fração geratriz da dízima:
A) 2,77…
B) 0,62626262…
C) 2,55…
D) 0,2666…
Eixo do Conhecimento: Números.
Eixo Cognitivo: Compreender e aplicar conceitos e procedimentos.
Cód. Habilidade: 9N1.11 – Identificar um número natural como primo, composto, “múltiplo/fator de” ou “divisor de” OU identificar a decomposição de um número natural em fatores primos OU relacionar as propriedades aritméticas (primo, composto, “múltiplo/fator de” ou “divisor de”) de um número natural à sua decomposição em fatores primos.
Questões:
23. (Sigma) Sobre múltiplos e divisores, marque a afirmação verdadeira.
A) 27 é múltiplo de 2.
B) 5 é múltiplo de 5 e de 3.
C) 20 é divisor de 20 e de 40.
D) 25 é múltiplo de 100 e de 30.
Eixo do Conhecimento: Números.
Eixo Cognitivo: Resolver problemas e argumentar.
Cód. Habilidade: 9N2.1 – Resolver problemas de adição, subtração, multiplicação, divisão, potenciação ou radiciação envolvendo números reais, inclusive notação científica.
Questões:
24. (CEFAF) A distância entre o Sol e a Lua é de aproximadamente 149.600.000 km. A representação deste número em notação científica equivale a
A) 1,496 ∙ 10 −9
B) 1,496 ∙ 10 −8
C) 1,496 ∙ 108
D) 1,496 ∙ 108
25. (SEPR). A capacidade do tanque de gasolina do carro de João é de 50 litros. As figuras mostram o medidor de gasolina do carro no momento de partida e no momento de chegada de uma viagem feita por João.
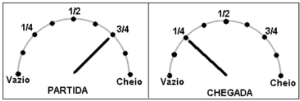
Quantos litros de gasolina ele gastou na viagem?
A) 12,5
B) 25
C) 37,5
D) 50
26. (SAEGO). Beatriz comprou uma boneca por R$ 79,50 e um jogo por R$ 33,50. Para pagar essa compra, ela deu R$ 200,00.
Quanto ela recebeu de troco?
A) R$ 197,00
B) R$ 113,00
C) R$ 97,00
D) R$ 87,00
Eixo do Conhecimento: Números.
Eixo Cognitivo: Resolver problemas e argumentar.
Cód. Habilidade: 9N2.2 – Resolver problemas de contagem cuja resolução envolva a aplicação do princípio multiplicativo.
Questões:
27. (SPAECE) Sr. Mário ganhou na loteria um carro novo. Na hora de receber o prêmio ficou sabendo que poderia fazer sua escolha entre 4 modelos diferentes: Gol, Fiesta, Pálio ou Corsa e também poderia escolher uma das 6 cores: azul, amarelo, verde, cinza, preto ou vermelho.
De quantas maneiras diferentes Sr. Mário poderá escolher o seu carro?
A) 10
B) 24
C) 34
D) 36
28. (Supletivo 2010). Na figura, abaixo, estão representadas três cidades pelos pontos P, R, S e as seis rodovias existentes, que interligam essas cidades.
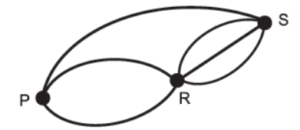
João partirá da cidade P em direção à cidade S.
Quantos trajetos diferentes João pode escolher para realizar essa viagem?
A) 3.
B) 6.
C) 7.
D) 9.
E) 12.
Eixo do Conhecimento: Números.
Eixo Cognitivo: Resolver problemas e argumentar.
Cód. Habilidade: 9N2.3 – Resolver problemas que envolvam porcentagens, incluindo os que lidam com acréscimos e decréscimos simples, aplicação de percentuais sucessivos e determinação das taxas percentuais.
Questões:
29. (SPAECE-CE) Priscila fez um empréstimo de R$ 4 500,00 para trocar seu carro. Após 6 meses, ela pagou esse empréstimo a uma taxa de juros simples de 1% ao mês.
Qual foi o valor total que Priscila pagou por esse empréstimo?
A) R$ 4 770,00
B) R$ 4 545,00
C) R$ 270,00
D) R$ 45,00
30. (SISPAE) Um vendedor ganha R$ 450,00 fixos por mês, mais 6% de comissão sobre suas vendas. No mês de março ele vendeu R$ 1.200,00 em mercadorias. Quanto recebeu no fim do mês?
A) R$ 500,00.
B) R$ 522,00.
C) R$ 1.110,00.
D) R$ 1.625,00.
31. (SAEB 2013) Na quarta série, os 13 meninos correspondem a 50% da turma. Assim, pode-se dizer que nesta 4ª série tem
A) 13 alunos
B) 26 alunos
C) 50 alunos
D) 63 alunos
Eixo do Conhecimento: Números.
Eixo Cognitivo: Resolver problemas e argumentar.
Cód. Habilidade: 9N2.4 – Resolver problemas que envolvam as ideias de múltiplo, divisor,máximo divisor comum ou mínimo múltiplo comum.
Questões:
32. (UFSC adaptado) No ponto de ônibus da Praça X passa um ônibus para a Linha Vermelha de 15 em 15 minutos e um ônibus para a Linha Amarela de 25 em 25 minutos.
Se os dois ônibus passaram juntos às 10 horas, qual o primeiro horário em que eles voltarão a passar juntos:
A) 10h:30min
B) 10h:45min
C) 11h:00min
D) 11h:15min
33. (NUCEPE) Para construir um painel, um marceneiro usa três ripas de madeira, de 2,40m, 2,80m e 3,20m de comprimento, respectivamente, que devem ser cortadas em pedaços de igual comprimento, no menor número possível de pedaços.
Qual deve ser o tamanho, em cm, de cada pedaço?
A) 12
B) 20
C) 30
D) 40
Eixo do Conhecimento: Álgebra.
Eixo Cognitivo: Compreender e aplicar conceitos e procedimentos.
Cód. Habilidade: 9A1.1 – Resolver uma equação polinomial de 1º grau.
Questões:
34. (AD-GO). Observe a equação apresentada abaixo.
2x + 2 = 8
Qual é o conjunto S solução dessa equação?
A) S = {3}.
B) S = {4}.
C) S = {5}.
D) S = {6}.
35. (Unesc 2024) Se Carlos considera que a equação 150x + 1200 descreve o gasto que ele terá com uma festa, de acordo com o número x de convidados, qual será a quantidade x se ele prevê um gasto total de R$ 21.450,00?
A) x = 135
B) x = 149
C) x = 86
D) x = 120
E) x = 250
Eixo do Conhecimento: Álgebra.
Eixo Cognitivo: Compreender e aplicar conceitos e procedimentos.
Cód. Habilidade: 9A1.2 – Inferir uma equação, inequação polinomial de 1º grau ou um sistema de equações de 1º grau com duas incógnitas que modela um problema.
Questões:
36. (UNIVIDA 2024) Em uma gincana escolar, a equipe de Joana marcou o triplo de pontos que a equipe de Miguel, e ainda ganhou um bônus de 132 pontos, alcançando um total de 396 pontos. Quantos pontos a equipe de Miguel marcou?
Alternativas
A) 85 pontos.
B) 88 pontos.
C) 92 pontos.
D) 80 pontos.
E) 95 pontos.
37. (SPAECE). Um número é maior do que outro 4 unidades e a soma desses dois números é 192. Se x é o menor desses números, então uma equação que permite calcular o valor de x é
A) x + 4 = 192
B) x + 4x = 192
C) x + (x − 4) = 192
D) x + (x + 4) = 192
38. (SARESP) O pen drive de Paulo possui 8 gigabytes e está totalmente ocupado por arquivos distribuídos em duas pastas, uma de músicas e outra de fotos. Dado que a pasta de fotos ocupa o triplo do espaço da pasta de músicas.
O sistema que expressa corretamente a relação entre o espaço ocupado pelas pastas no pen drive é
A)![]()
B)![]()
C)![]()
D)![]()
Eixo do Conhecimento: Álgebra.
Eixo Cognitivo: Compreender e aplicar conceitos e procedimentos.
Cód. Habilidade: 9A1.3 – Identificar uma representação algébrica para o padrão ou a regularidade de uma sequência de números racionais OU representar algebricamente o padrão ou a regularidade de Uma sequência de números racionais.
Questões:
39. (Prova Brasil) As figuras mostradas abaixo estão organizadas dentro de um padrão que se repete.
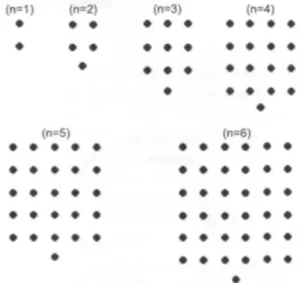
Mantendo esta disposição, a expressão algébrica que representa o número de pontos N em função da ordem n (n = 1, 2, …) é:
A) N = n +1.
B) N = n² – 1.
C) N = 2n +1
D) N = n² +1
40. (AD-GO) Observe, no quadro abaixo, os termos de uma sequência numérica com suas posições enumeradas.
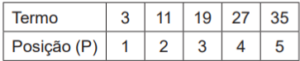
Uma expressão algébrica que modela cada termo dessa sequência, a partir da posição P que ele ocupa, é
A) 8P.
B) 3 + 8P.
C) 8P – 5.
D) (P – 1) + 8
41. (Saresp 2007). Considere a seqüência:
3; 7; 11; 15; 19; 23; … ; n; …
O número que vem imediatamente depois de n pode ser representado por:
A) n + 1
B) n + 4
C) 24
D) 4n
Eixo do Conhecimento: Álgebra.
Eixo Cognitivo: Compreender e aplicar conceitos e procedimentos.
Cód. Habilidade: 9A1.4 – Identificar representações algébricas equivalentes.
Questões:
42. (Saresp) Observe a expressão algébrica a seguir, sendo x ≠ 0:
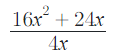
Assinale a alternativa que representa corretamente a simplificação da expressão
A) 4x+24x
B) 16x+6x
C) 4+6x
D) 4x+6
43. (AD-GO) Observe a expressão algébrica apresentada no quadro abaixo, sendo x ≠ 0.
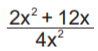
Uma forma fatorada e simplificada dessa expressão está apresentada em
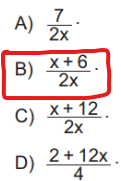
Eixo do Conhecimento: Álgebra.
Eixo Cognitivo: Compreender e aplicar conceitos e procedimentos.
Cód. Habilidade: 9A1.5 – Associar uma equação polinomial de 1º grau com duas variáveis auma reta no plano cartesiano.
Questões:
44. (Saresp 2007) A reta r, representada no plano cartesiano da figura, corta o eixo y no ponto (0, 4) e corta o eixo x no ponto (–2, 0).
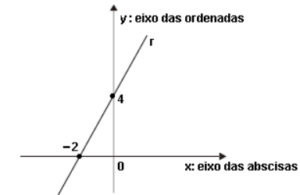
Qual é a equação dessa reta?
A) y = x + 4
B) y = 4x + 2
C) y = x – 2
D) y = 2x + 4
45. (Supletivo 2012 – MG) Observe a equação linear com duas incógnitas apresentada abaixo.
y + 0,5x = 4
Qual é a reta que corresponde à equação apresentada?
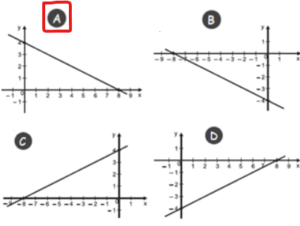
Eixo do Conhecimento: Álgebra.
Eixo Cognitivo: Compreender e aplicar conceitos e procedimentos.
Cód. Habilidade: 9A1.6 – Inferir uma equação polinomial de 2º grau que modela um problema.
Questões:
46. (Saresp – adaptdado) O retângulo representado na figura tem 35 m2 de área.
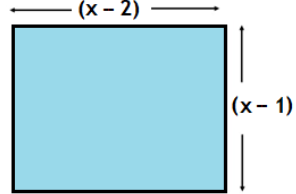
A equação polinomial do segundo grau que permite calcular o valor de x, (comprimento do lado do quadrado), é:
A) x2 + 8x – 20 = 0
B) x2 – 8x – 50 = 0
C) x2 – 2x + 50 = 0
D) x2 + 2x + 20 = 0
47. (SAERJ-adaptado) José planta alface em um canteiro quadrado. Ele verificou que, se aumentasse 3 m nas duas dimensões, como mostra a figura abaixo, a área plantada passaria a ter 64 m2.
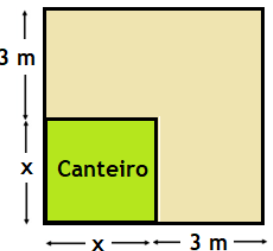
A equação polinomial do segundo grau que permite calcular o valor de x, (comprimento do lado do canteiro), é:
A) x2 + 6x – 64 = 0
B) x2 + 6x – 55 = 0
C) x2 + 6x + 73 = 0
D) x2 + 3x + 55 = 0
Eixo do Conhecimento: Álgebra.
Eixo Cognitivo: Compreender e aplicar conceitos e procedimentos.
Cód. Habilidade: 9A1.7 – Resolver uma equação polinomial de 2º grau.
Questões:
48. (CAED-MEC) Observe a equação polinomial apresentada abaixo.
x2 + 8x – 9 = 0
Qual é o conjunto solução S dessa equação?
A) S = {– 54, 46}.
B) S = {– 29, 21}.
C) S = {– 18, 2}.
D) S = {– 9, 1}.
49. (IFSULDEMINAS) Observe a equação polinomial apresentada abaixo.
x2 – 8x + 7 = 0
Qual é o conjunto solução S dessa equação?
A) S = {0, 1}.
B) S = {0, 7}.
C) S = {1, 7}.
D) S = {7, 8}.
50. (UF-ES) A equação x2 – 10x + 25 = 0 tem as seguintes soluções no conjunto dos números reais:
A) somente 5.
B) somente 10.
C) – 5.
D) 5 e 10.
Eixo do Conhecimento: Álgebra.
Eixo Cognitivo: Compreender e aplicar conceitos e procedimentos.
Cód. Habilidade: 9A1.8 – Associar uma das representações de uma função afim ou quadrática a outra de suas representações (tabular, algébrica, gráfica) OU associar uma situação que envolva função afim ouquadrática a uma das suas representações (tabular, algébrica, gráfica).
Questões:
51. (APA – Crede-CE) Seu Raimundo é dono de um táxi e cobra uma corrida da seguinte maneira: um valor fixo de R$ 5,00 mais R$ 0,80 por cada quilômetro percorrido.
Sendo y o valor a pagar e x o número de quilômetros, a função que permite calcular a tarifa final de uma corrida do táxi é
A) y = 5 + 0,80x
B) y = 5x + 0,80
C) y = 5 – 0,80x
D) y = 4,20 + 0,80x
52. (SPAECE) Observe abaixo o gráfico de uma função polinomial do 1° grau.
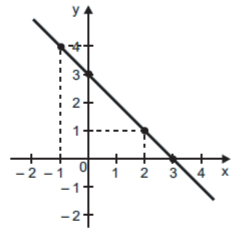
Qual é a lei de formação dessa função?
A) f(x) = − 3x + 3
B) f(x) = − x + 4
C) f(x) = − x + 3
D) f(x) = 2x + 1
E) f(x) = 3x + 3
53. (SAEGO) O gráfico abaixo representa uma função do 1° grau.
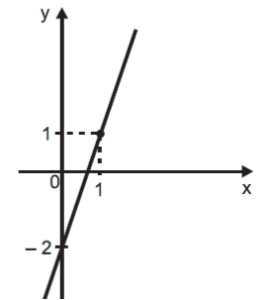
A representação algébrica dessa função é
A) y = x + 1
B) y = x – 2
C) y = –2x + 1
D) y = 3x – 2
Eixo do Conhecimento: Álgebra.
Eixo Cognitivo: Resolver problemas e argumentar.
Cód. Habilidade: 9A2.1 – Resolver problemas que envolvam variação de proporcionalidade direta ou inversa entre duas ou mais grandezas, inclusive escalas, divisões proporcionais e taxa de variação.
Questões:
54. (AD-GO) Uma empresa gasta 18 dias para produzir um lote de bancos de plástico utilizando 2 máquinas iguais que funcionam juntas todos os dias por um mesmo período de tempo. O dono dessa empresa comprou uma máquina igual às outras e irá colocar as 3 para funcionarem juntas todos os dias por esse mesmo período de tempo.
Quantos dias essas 3 máquinas gastarão para produzir um lote de bancos de plástico?
A) 12 dias.
B) 17 dias.
C) 18 dias.
D) 27 dias.
55. (SEAMA) Em uma fazenda, 12 tratores trabalhando no mesmo ritmo colhem uma quantidade de milho em 60 horas.
Para colher essa mesma quantidade de milho em 40 horas, quantos desses tratores, trabalhando nesse mesmo ritmo, seriam necessários?
A) 8
B) 10
C) 18
D) 32
56. (SISPAE) Um salão foi reservado para um evento cultural. Os convidados ficarão em pé numa área de 600 metros quadrados. Sabe-se que, por motivos de segurança, foram calculadas 4 pessoas por metro quadrado.
O número máximo de pessoas que poderão entrar no salão, seguindo as normas de segurança, é
A) 200.
B) 240.
C) 2400.
D) 4800.
57. (Prova Brasil) O desenho de um colégio foi feito na seguinte escala: cada 4 cm equivale a 5 m.
A representação ficou com 10 cm de altura. Qual é a altura real, em metros, do colégio?
A) 2,0
B) 12,5
C) 50,0
D) 125,0
Eixo do Conhecimento: Álgebra.
Eixo Cognitivo: Resolver problemas e argumentar.
Cód. Habilidade: 9A2.2: Resolver problemas que envolvam cálculo do valor numérico de expressões algébricas.
Questões:
58. (SEDUC-GO) O número de diagonais de um polígono é calculado com o uso da expressão 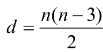 , sendo d o número de diagonais e n o número de lados do polígono. O número de diagonais de um polígono de 5 lados é:
, sendo d o número de diagonais e n o número de lados do polígono. O número de diagonais de um polígono de 5 lados é:
A) 4
B) 5
C) 6
D) 7
59. (SAEP 2013). Na escola de Marcos Antonio são realizadas duas avaliações por bimestre, sendo que a primeira tem peso um e a segunda tem peso dois, usando a seguinte formula:
![]()
onde A1 é o valor da primeira avaliação e A2 é o valor da segunda avaliação.
Se Marcos Antonio tirou 5,6 na primeira avaliação e 9,2 na segunda avaliação, a sua média do bimestre em questão foi
A) 8,0.
B) 7,4.
C) 6,8.
D) 5,0.
60.
(SAEP 2013). Você sabia?
No ano de 1916, as Olimpíadas deveriam ocorrer na Alemanha, porém, em função da Primeira Guerra Mundial, os Jogos Olímpicos foram cancelados.
Em função da Segunda Guerra Mundial, os Jogos Olímpicos de 1940 e 1944 também foram cancelados.
XIV Olimpíada, foram os Jogos Olímpicos realizados pela segunda vez em Londres – após doze anos de interrupção devido à II Guerra Mundial.
As edições voltaram a ocorrer a partir de 1948.
http://pt.wikipedia.org/wiki/Jogos
A expressão algébrica que representa a regularidade das realizações das Olimpíadas no mundo pós-guerra é Ar = 1948 + 4(N – 1), sendo Ar o ano de realização e N o número de edição. O ano que corresponde a realização da 18ª Olimpíadas pós-guerra é
A) 2016.
B) 2014.
C) 2020.
D) 2024.
Eixo do Conhecimento: Álgebra.
Eixo Cognitivo: Resolver problemas e argumentar.
Cód. Habilidade: 9A2.3:Resolver problemas que possam ser representados por sistema deequações de 1º grau com duas incógnitas.
Questões:
61. (Cefet – RJ – 2016). Uma garrafa PET (politereftalato de etileno) com sua tampa custa sessenta centavos. Sabendo que a garrafa custa cinquenta centavos a mais que a tampa, quanto custa só a tampa?
A) R$ 0,05
B) R$ 0,15
C) R$ 0,25
D) R$ 0,35
62. (3ª P.D – SEDUC-GO). Durante os jogos interclasse, Karen foi até a lanchonete e comprou um suco e um salgado por R$ 3,20. Raul comprou dois sucos e um salgado por R$ 4,20.
A quantidade de sucos e salgados comprados por Karen foram, respectivamente, de:
A) R$ 1,00 e R$ 2,20.
B) R$ 2,20 e R$ 1,00.
C) R$ 1,50 e R$ 1,70.
D) R$ 2,00 e R$ 1,20.
63. (SEPR). No início de uma festa, tinham 200 jovens. Depois o número de rapazes dobrou e o de moças aumentou 40. Com isso o número de rapazes ficou o mesmo que o de moças.
Quantos rapazes e quantas moças havia no início da festa?
A) 80 rapazes e 120 moças.
B) 120 rapazes e 80 moças.
C) 160 rapazes e 120 moças.
D) 160 rapazes e 160 moças.
Eixo do Conhecimento: Álgebra.
Eixo Cognitivo: Resolver problemas e argumentar.
Cód. Habilidade: 9A2.4: Resolver problemas que possam ser representados por equações polinomiais de 2º grau.
Questões:
64. (Prova Brasil) O custo de uma produção, em milhares de reais, de x máquinas iguais é dado pela expressão C(x) = x² – x + 10. Se o custo foi de 52 mil reais, então, o número de máquinas utilizadas na produção foi;
A) 6
B) 7.
C) 8.
D) 9.
65. (SAERJ) Rose multiplicou a idade atual de seu filho pela idade que ele terá daqui a 5 anos e obteve como resultado 14 anos.
Qual é a idade atual do filho de Rose?
A) 2 anos.
B) 5 anos.
C) 7 anos.
D) 9 anos.
66. (Saresp 2007) Se Eduardo acertasse os números que são as respostas a um desafio, sua tia daria a ele, em reais, o maior valor entre as respostas do desafio.

Eduardo acertou e recebeu de sua tia
A) 20 reais
B) 12 reais
C) 10 reais
D) 8 reais
Eixo do Conhecimento: Álgebra.
Eixo Cognitivo: Resolver problemas e argumentar.
Cód. Habilidade: 9A2.5:Resolver problemas que envolvam função afim.
Questões:
67. (SAEPE) Uma empresa de arquitetura paga o salário de seus funcionários de acordo com a função apresentada no quadro abaixo.
y = 2 230 + 1 100x
Nessa função, y representa o salário mensal pago pela empresa de arquitetura ao profissional e x é o número de projetos desse funcionário que foram aprovados no mês.
Qual foi o salário de um profissional que teve 3 de seus projetos aprovados em um mês?
A) R$ 2 230,00
B) R$ 3 300,00
C) R$ 3 330,00
D) R$ 5 530,00
68. (Saeb) Um padeiro fabrica 250 pães por hora. A função que representa a quantidade de pães fabricados P em função do tempo t em horas é
A) P(t) = 250 + t
B) P(t) = 250/t
C) P(t) = 250 – t
D) P(t) = 250t
69. (Saresp-2010) Uma livraria comprou muitos exemplares de certo livro, pagando por cada exemplar o valor de R$ 30,00, pagou ainda R$ 300,00 pelo transporte da mercadoria até a sua sede. Sabendo que cada livro comprado da editora foi revendido pela livraria por R$ 40,00 e que o lucro resultante, ao final da revenda, foi de R$ 1.200,00, é correto afirmar que o número de exemplares comprados inicialmente pela livraria foi de
A) 150.
B) 120.
C) 100.
D) 80.
Eixo do Conhecimento: Geometria.
Eixo Cognitivo: Compreender e aplicar conceitos e procedimentos.
Cód. Habilidade: 9G1.1: Identificar, no plano cartesiano, figuras obtidas por uma ou mais transformações geométricas (reflexão, translação, rotação).
Questões:
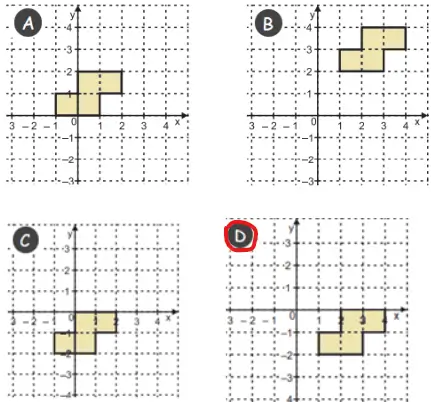
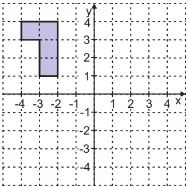
70. (MEC-CAED)Observe a figura apresentada no plano cartesiano abaixo.
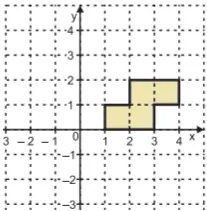
Ao transladar essa figura em duas unidades no sentido negativo do eixo y, obtém-se
71. (MEC-CAED). Observe a figura representada no plano cartesiano abaixo.
O resultado da reflexão dessa figura em relação ao eixo x está representado em
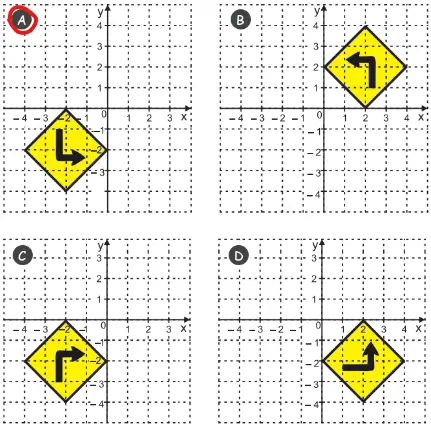
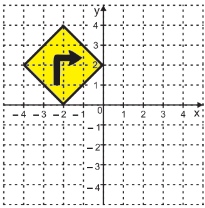
72. (MEC-CAED). Observe a figura apresentada no plano cartesiano abaixo.
Ao rotacionar essa figura em relação à origem, 180° no sentido horário, obtém-se
Eixo do Conhecimento: Geometria.
Eixo Cognitivo: Compreender e aplicar conceitos e procedimentos.
Cód. Habilidade: 9G1.2:Relacionar o número de vértices, faces ou arestas de prismas ou pirâmides, em função do seu polígono da base.
Questões:
73. (SEAPE). Observe a figura abaixo.
Quantos vértices tem essa figura?
A) 24
B) 18
C) 12
D) 10
74. (SAEPE) Gilberto ganhou uma caixa com a forma indicada no desenho abaixo.
Quantas arestas possui essa caixa?
A) 6
B) 8
C) 12
D) 18
75. (SEME) Leandro faz coleção de dados. Um desses dados tem o formato de um tetraedro regular, cujas faces são formadas por 4 triângulos equiláteros.
O número de vértices desse poliedro é
A) 18
B) 12
C) 10
D) 4
Eixo do Conhecimento: Geometria.
Eixo Cognitivo: Compreender e aplicar conceitos e procedimentos.
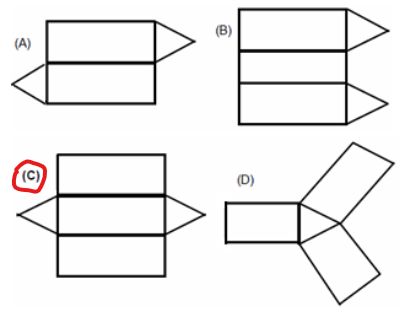
Cód. Habilidade: 9G1.3: Relacionar objetos tridimensionais às suas planificações ou vistas.
Questões:
76. (Prova Brasil) É comum encontrar em acampamentos barracas com fundo e que têm a forma apresentada na figura abaixo.
Qual desenho representa a planificação dessa barraca?
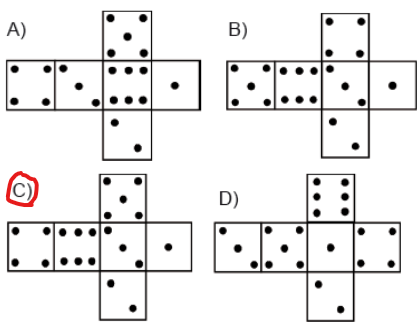
77. (SPEACE). Observe o dado representado pela figura abaixo.

Que planificação corresponde a esse dado?
Eixo do Conhecimento: Geometria.
Eixo Cognitivo: Compreender e aplicar conceitos e procedimentos.
Cód. Habilidade: 9G1.4: Classificar polígonos em regulares e não regulares.
Questões:
78. (SME-GO) Um polígono com todos os lados e ângulos iguais é chamado de
A) regular.
B) irregular.
C) côncavo.
D) convexo.
79. Observe os polígonos a seguir:
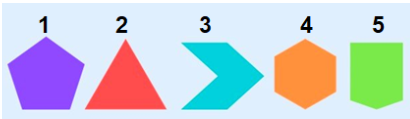
A opção que indica somente polígonos regulares é:
A) 1, 2 e 3
B) 2, 4 e 5
C) 1, 2 e 4
D) 1, 2 e 5
Eixo do Conhecimento: Geometria.
Eixo Cognitivo: Compreender e aplicar conceitos e procedimentos.
Cód. Habilidade: 9G1.5: Identificar propriedades e relações existentes entre os elementos de um triângulo (condição de existência, relações de ordem entre as medidas dos lados e as medidas dos ângulos internos, soma dos ângulos internos, determinação da medida de um ângulo interno ou externo).
Questões:
80. (S.P.Joinvile) A medida x indicada na figura abaixo representa:
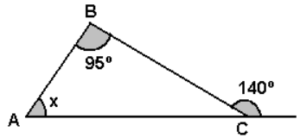
A) 45°
B) 40°
C) 235°
D) 70°
81. (Saerjinho). Os lados de um triângulo são representados por a, b e c e, os ângulos opostos a eles medem respectivamente 80°, 70° e 30°.
A relação entre a, b e c é
A) a < b < c
B) b < c < a
C) c < b < a
D) b < a < c
Eixo do Conhecimento: Geometria.
Eixo Cognitivo: Compreender e aplicar conceitos e procedimentos.
Cód. Habilidade: 9G1.6:Classificar triângulos ou quadriláteros em relação aos lados ou aos ângulos internos.
Questões:
82. (SAEGO-2012 – Adaptado) Patrícia na aula de artes desenhou um barquinho como representado na figura abaixo:
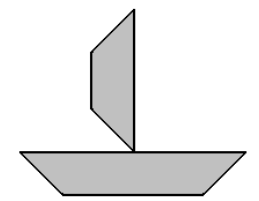
O quadrilátero que Patrícia utilizou no seu desenho é
A) quadrado
B) retângulo
C) paralelogramo
D) trapézio.
83. (SEDUC-GO) Observe os quadriláteros:
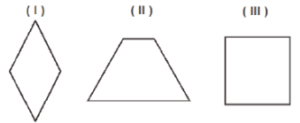
Identifique a alternativa que expressa os nomes dos quadriláteros (I), (II) e (III) exatamente nessa ordem.
A) Triângulo, trapézio e quadrado.
B) Losango, trapézio e quadrado.
C) Losango, retângulo e quadrado.
D) Losango, retângulo e quadrado.
Eixo do Conhecimento: Geometria.
Eixo Cognitivo: Compreender e aplicar conceitos e procedimentos.
Cód. Habilidade: 9G1.7:Reconhecer polígonos semelhantes ou as relações existentes entre ângulos e lados correspondentes nesses tipos de polígonos.
Questões:
84. (Prova Brasil) Observe a figura abaixo.
Considere o lado de cada quadradinho como unidade de medida de comprimento.
Para que o perímetro do retângulo seja reduzido à metade, a medida de cada lado deverá ser
A) dividida por 2.
B) multiplicada por 2.
C) aumentada em 2 unidades.
D) dividida por 3.
85. (Saerjinho) Nas malhas quadriculadas, com quadradinhos de mesmo tamanho, você vê, na cor cinza, as figuras P e Q.
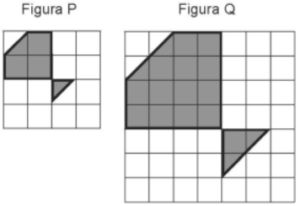
A figura Q é uma ampliação da figura P. Quantas vezes a área da figura Q é maior que a área da figura P?
A) 2
B) 3
C) 4
D) 5
Eixo do Conhecimento: Geometria.
Eixo Cognitivo: Compreender e aplicar conceitos e procedimentos.
Cód. Habilidade: 9G1.8: Reconhecer circunferência/círculo como lugares geométricos, seus elementos (centro, raio, diâmetro, corda, arco, ângulo central, ângulo inscrito).
Questões:
86. (CAED) Observe, no quadro abaixo, as representações de algumas figuras geométricas.
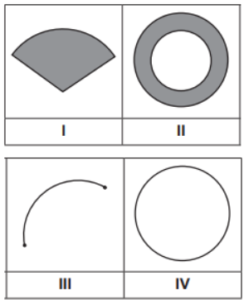
Nesse quadro, uma coroa circular pode estar indicada por
A) I.
B) II.
C) III.
D) IV.
87. (SAERS) Observe abaixo a circunferência de centro P.
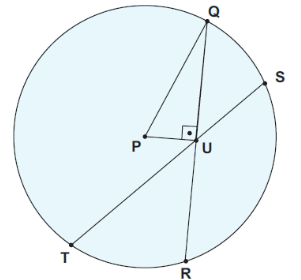
A medida do diâmetro dessa circunferência é
A) 2 · PQ.
B) 2 · PU.
C) QR.
D) 2 · QU.
88. (Prova Brasil) Observe a circunferência de centro em P.
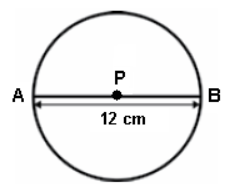
A medida do segmento PB é
A) 2 cm.
B) 3 cm.
C) 6 cm.
D) 36 cm.
Eixo do Conhecimento: Geometria.
Eixo Cognitivo: Compreender e aplicar conceitos e procedimentos.
Cód. Habilidade: 9G1.9: Identificar retas ou segmentos de retas concorrentes, paralelos ou perpendiculares.
Questões:
89. (CFTMG 2014) A figura a seguir representa uma cadeira onde o assento é um paralelogramo perpendicular ao encosto.
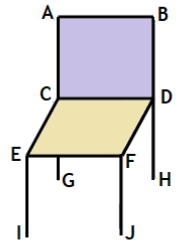
A partir dos pontos dados, é correto afirmar que os segmentos de retas
A) CD e EF são paralelos.
B) BD e FJ são concorrentes.
C) AC e CD são coincidentes.
D) AB e EI são perpendiculares.
90. (CFTMG) Observe a imagem abaixo:
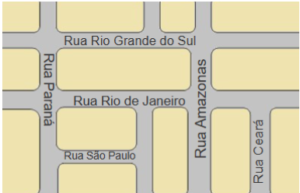
Josué se mudou para uma nova cidade com sua família. Ele ainda não conhece muito bem o bairro. Ele está se guiando pelo mapa.
As ruas Paraná e Rio Grande do Sul no mapa são retas
A) concorrentes.
B) paralelas.
C) perpendiculares.
D) transversais.
Eixo do Conhecimento: Geometria.
Eixo Cognitivo: Compreender e aplicar conceitos e procedimentos.
Cód. Habilidade: 9G1.10: Identificar relações entre ângulos formados por retas paralelas cortadas por uma transversal.
Questões:
91. (AD-GO) Observe os ângulos formados pela interseção das retas paralelas r e s com a reta transversal t, apresentados na figura abaixo.
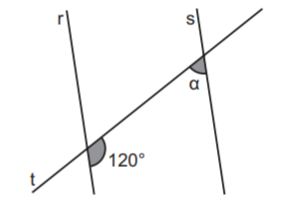
A medida do ângulo α, em grau, é
A) 30°.
B) 60°.
C) 120°.
D) 180°.
92. (Portal Obmep) Observe os ângulos entre as retas paralelas “r” “e “s” com a transversal “t”.
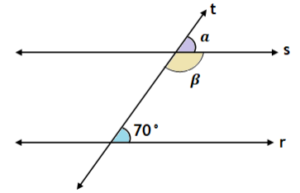
A medida dos ângulos indicado pelas letras gregas α e β, respectivamente, é:
A) 70° e 80°.
B) 110° e 70°.
C) 70° e 110°.
D) 70° e 100°.
Eixo do Conhecimento: Geometria.
Eixo Cognitivo: Resolver problemas e argumentar.
Cód. Habilidade: 9G2.1: Descrever OU esboçar o deslocamento de pessoas e/ou de objetos em representações bidimensionais (mapas, croquis etc.), plantas de ambientes ou vistas, de acordo com condições dadas.
Questões:
93. (Prova Brasil) Num tabuleiro de xadrez, jogamos com várias peças que se movimentam de maneiras diferentes. O cavalo se move para qualquer casa que possa alcançar com movimento na forma de “L”, de três casas. Na figura abaixo, os pontos marcados representam as casas que o cavalo pode alcançar, estando na casa d4.

Dentre as casas que o cavalo poderá alcançar, partindo da casa f5 e fazendo uma única jogada, estão:
A) g3 ou d6
B) h5 ou f3
C) h7 ou d7
D) d3 ou d7
94. (SAERS) Lucas e seus amigos saem do ponto A, em direção à praia. Na primeira bifurcação, eles pegam o caminho à sua direita; na segunda bifurcação eles pegam o caminho à sua esquerda e na terceira bifurcação eles escolhem o caminho à sua direita.
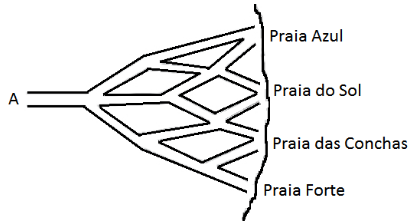
Em que praia eles chegam?
A) Praia Azul.
B) Praia do Sol.
C) Praia das Conchas.
D) Praia Forte.
Eixo do Conhecimento: Geometria.
Eixo Cognitivo: Resolver problemas e argumentar.
Cód. Habilidade: 9G2.2: Construir/desenhar figuras geométricas planas ou espaciais que satisfaçam condições dadas.
Questões:
Em breve!
Eixo do Conhecimento: Geometria.
Eixo Cognitivo: Resolver problemas e argumentar.
Cód. Habilidade: 9G2.3: Resolver problemas que envolvam relações entre ângulos formados por retas paralelas cortadas por uma transversal, ângulos internos ou externos de polígonos ou cevianas (altura, bissetriz, mediana, mediatriz) de polígonos.
Questões:
95. (SIMAVE) A logomarca de uma empresa é formada por um hexágono regular, um trapézio retângulo e um quadrado, como mostra a figura abaixo.
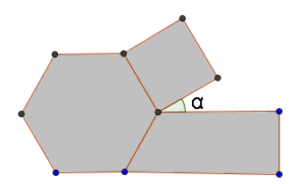
Quanto mede o ângulo α, indicado nessa figura?
A) 30°
B) 45°
C) 60°
D) 90°
96. (SPAECE) Lucas desenhou uma figura formada por dois hexágonos. Veja o que ele desenhou.
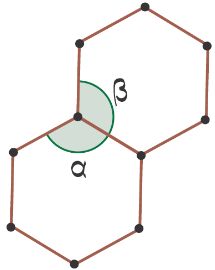
Nessa figura, a soma das medidas dos ângulos α e β é:
A) 60°
B) 120°
C) 240°
D) 720°
Eixo do Conhecimento: Geometria.
Eixo Cognitivo: Resolver problemas e argumentar.
Cód. Habilidade: 9G2.4: Resolver problemas que envolvam relações métricas do triângulo retângulo, incluindo o teorema de Pitágoras.
Questões:
97. (SAEPI) Durante a reforma de uma cobertura, a empreiteira responsável instalou uma rampa de madeira para depositar o entulho da obra diretamente na caçamba, conforme ilustra o desenho abaixo.
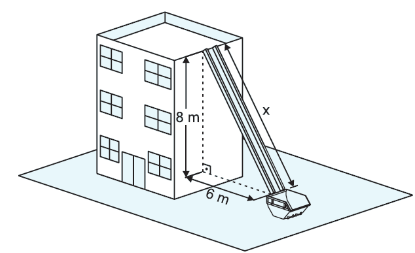
Qual é a medida x do comprimento da madeira utilizada para construção dessa rampa?
A) 10 m
B) 14 m
C) 50 m
D) 100 m
98. (OBMEP) Uma formiga está no ponto A da malha mostrada na figura. A malha é formada por retângulos de 3 cm de largura por 4 cm de comprimento. A formiga só pode caminhar sobre os lados ou sobre as diagonais dos retângulos. Qual é a menor distância que a formiga deve percorrer para ir de A até B?

A) 12 cm.
B) 14 cm.
C) 15 cm.
D) 18 cm.
Eixo do Conhecimento: Geometria.
Eixo Cognitivo: Resolver problemas e argumentar.
Cód. Habilidade: 9G2.5: Resolver problemas que envolvam polígonos semelhantes.
Questões:
99. (Saerjinho) Observe os retângulo e as medidas de seus lados.
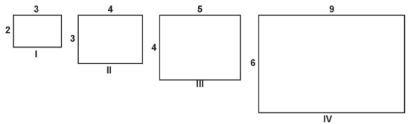
Qual é o par de retângulo semelhantes?
A) I e IV
B) II e III
C) II e IV
D) III e IV
100. (GAVE) O triângulo PQR é uma redução do triângulo equilátero ABC, de razão 0,5. Sabendo que QR = 5.
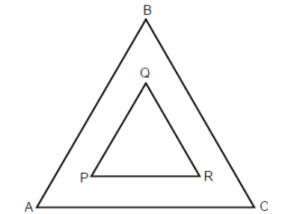
O valor o lado do triângulo ABC é
A) 2,5 cm.
B) 5 cm.
C) 7,5 cm.
D) 10 cm.
Eixo do Conhecimento: Geometria.
Eixo Cognitivo: Resolver problemas e argumentar.
Cód. Habilidade: 9G2.6:Resolver problemas que envolvam aplicação das relações de proporcionalidade abrangendo retas paralelas cortadas por transversais.
Questões:
101. (Enem) A planta de determinado bairro de uma cidade apresentou o desenho a seguir. O responsável pelo departamento de obras do município constatou a ausência de algumas medidas nessa planta, as quais ele representou no projeto por x e y.
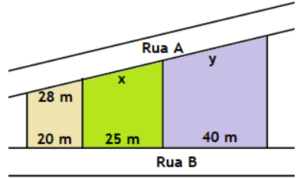
Com base nos dados do projeto, esse responsável pôde calcular corretamente os respectivos valores de x e y:
A) 35 m e 56 m
B) 25 m e 40 m
C) 35 m e 70 m
D) 56 m e 70 m
102. (Uff 2002). O circuito triangular de uma corrida está esquematizado na figura a seguir:
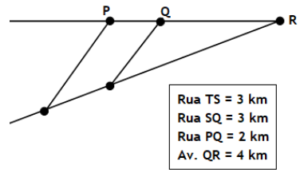
As ruas TP e SQ são paralelas. Partindo de S, cada corredor deve percorrer o circuito passando, sucessivamente, por R, Q, P, T, retornando, finalmente, a S.
O comprimento do segmento SR é:
A) 4 km
B) 5 km
C) 6 km
D) 7 km
Eixo do Conhecimento: Geometria.
Eixo Cognitivo: Resolver problemas e argumentar.
Cód. Habilidade: 9G2.7: Resolver problemas que envolvam relações entre os elementos de uma circunferência/círculo (raio, diâmetro, corda, arco, ângulo central, ângulo inscrito).
Questões:
103. (PAEBES) O triângulo abaixo foi construído unindo-se os centros de três circunferências tangentes de 5 cm de raio.
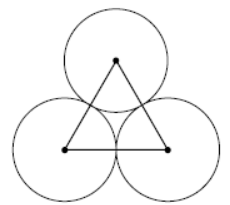
Quanto mede cada lado desse triângulo?
A) 30 cm
B) 20 cm
C) 15 cm
D) 10 cm
104. (SAEP 2013) A figura abaixo mostra o pneu de uma bicicleta. Joãozinho com suas ideias miraculosas quer retirar todos os raios, cortar o aro da bicicleta para esticá-lo e usar em uma das suas engenhocas como mostra na figura abaixo.
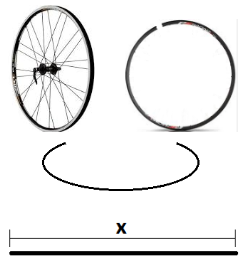
Após ele desfazer o círculo que o aro da bicicleta formava, o valor de x corresponde
A) ao raio da circunferência.
B) ao arco da circunferência.
C) ao diâmetro da circunferência.
D) ao comprimento da circunferência.
Eixo do Conhecimento: Geometria.
Eixo Cognitivo: Resolver problemas e argumentar.
Cód. Habilidade: 9G2.8:Determinar o ponto médio de um segmento de reta ou a distância entre dois pontos quaisquer, dadas as coordenadas desses pontos no plano cartesiano.
Questões:
105. Marcos gosta de mapear estrelas em um pequeno segmento do céu usando um sistema de coordenadas cartesianas. Ele identificou duas estrelas brilhantes A e B e anotou suas coordenadas no plano a seguir.
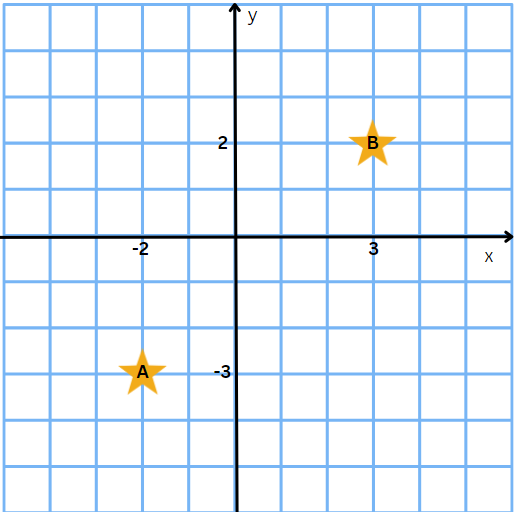
Recentemente, ele identificou uma nova estrela que está exatamente no ponto médio entre as estrelas A e B.
Quais as coordenadas (x,y) da nova estrela identificada por Marcos?
A) (1,-1).
B) (1/2,-1/2).
C) (-5,-5).
D) (-3,1/2).
Eixo do Conhecimento: Grandezas e medidas.
Eixo Cognitivo: Resolver problemas e argumentar.
Cód. Habilidade: 9M2.1: Resolver problemas que envolvam medidas de grandezas (comprimento, massa, tempo, temperatura, capacidade ou volume)em que haja conversões entre unidades mais usuais.
Questões:
106. (SAEB 2013) Foi feita a medição do comprimento da parede de uma sala, utilizando, como instrumento de medida, uma fita métrica de apenas 80 cm. Essa medição correspondeu a 5 medidas e meia da fita. Quantos metros de comprimento tem a parede?
A) 4,4 m
B) 4,5 m
C) 8,0 m
D) 8,5 m
107. (SAEB 2013) Uma garrafa de refrigerante tem 1,5 litros de capacidade. Para comprarmos 9 litros deste refrigerante devemos pedir
A) 6 garrafas.
B) 7 garrafas.
C) 7,5 garrafas.
D) 8 garrafas.
108. (SAERS) Na casa de João há uma piscina com capacidade para 25,5 m³ de água.
A capacidade de água, em litros, dessa piscina é
A) 255.
B) 2 550.
C) 25 500.
D) 255 000.
109. (SAEPE) Laura comprou 300 g de queijo, 200 g de presunto, 400 g de pão e 1 kg de laranja. Ela colocou todos esses produtos em uma mesma sacola plástica.
No total, quantos quilogramas de produtos Laura colocou nessa sacola?
A) 1 900.
B) 901.
C) 900.
D) 1,9.
E) 1,0.
Eixo do Conhecimento: Grandezas e medidas.
Eixo Cognitivo: Resolver problemas e argumentar.
Cód. Habilidade: 9M2.2: Resolver problemas que envolvam perímetro de figuras planas.
Questões:
110. (AD-GO) Para refazer a instalação elétrica em seu restaurante, Valdir comprou, em uma loja, uma quantidade de fio equivalente ao dobro da medida do perímetro desse restaurante. Observe abaixo a planta do restaurante de Valdir e algumas medidas indicadas.
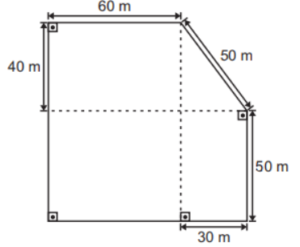
Quantos metros de fio Valdir comprou nessa loja para refazer a instalação elétrica de seu restaurante?
A) 460 m.
B) 680 m.
C) 720 m.
D) 860 m.
111. (AD-GO) Para a construção de um estacionamento, será construído um muro em todo o contorno do terreno, exceto na entrada reservada aos veículos, conforme representado na figura abaixo.
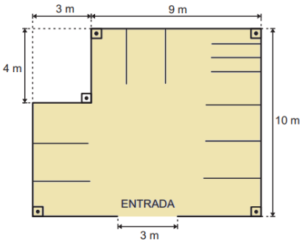
Qual é o comprimento do muro, em metro, que será construído no contorno desse terreno?
A) 29 m.
B) 34 m.
C) 38 m.
D) 41 m.
Eixo do Conhecimento: Grandezas e medidas.
Eixo Cognitivo: Resolver problemas e argumentar.
Cód. Habilidade: 9M2.3: Resolver problemas que envolvam área de figuras planas.
Questões:
112. (SAEGO) A figura abaixo representa o chão de uma empresa que está sendo reformada.
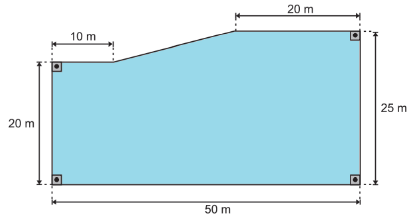
Quantos metros quadrados de piso, no mínimo, deverão ser comprados para cobrir todo o chão dessa empresa?
A) 1 100
B) 1 150
C) 1 200
D) 1 250
113. (PAEBES) Uma empresa que fabrica peças em aço foi contratada para produzir um logotipo cujo formato é o de uma justaposição de um triângulo a um semicírculo.
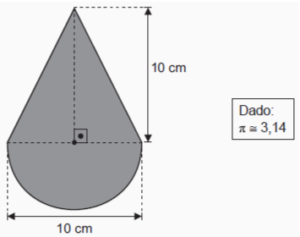
Nesse logotipo, a medida do diâmetro do semicírculo é igual a medida da base do triângulo. A figura abaixo apresenta o desenho desse logotipo com algumas de suas medidas.
Qual foi a quantidade de aço utilizada por essa empresa para produzir esse logotipo?
A) 65,70 cm2.
B) 89,25 cm2.
C) 100,00 cm2.
D) 207,00 cm2.
Eixo do Conhecimento: Grandezas e medidas.
Eixo Cognitivo: Resolver problemas e argumentar.
Cód. Habilidade: 9M2.4: Resolver problemas que envolvam volume de prismas retos ou cilindros retos.
Questões:
114. (SARESP) Na figura seguinte, cada cubinho que compõe o cubo mágico possui um volume de 1 cm³.

O volume total, em cm³, desse cubo mágico é de
A) 6.
B) 36.
C) 108.
D) 216.
115. (SAEMI) Uma substância estava armazenada em um recipiente no formato de um paralelepípedo retângulo e ocupava toda a capacidade desse recipiente. Essa substância foi completamente transferida para um recipiente de formato cilíndrico. As medidas internas desses dois recipientes estão indicadas no desenho abaixo.
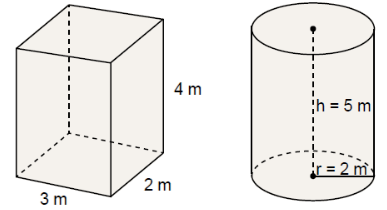
Considere: π = 3,14.
Qual é a capacidade máxima restante desse cilindro após a transferência dessa substância?
A) 38,8 m3
B) 50,2 m3
C) 62,8 m3
D) 86,8 m3
Eixo do Conhecimento: Probabilidade e estatística.
Eixo Cognitivo: Compreender e aplicar conceitos e procedimentos.
Cód. Habilidade: 9E1.1: Identificar os indivíduos (universo ou população-alvo da pesquisa),as variáveis e os tipos de variáveis (quantitativas ou categóricas) em um conjunto de dados.
Questões:
116. (UFSC) Observe algumas variáveis a seguir:
I. número de filhos dos atuais alunos da UFSC.
II. número de leitos hospitalares de uma relação de hospitais.
III. número de alunos cursando estatística.
IV. número de anos de estudo dos atuais alunos da UFSC.
V. material das paredes dos domicílios (alvenaria, taipa, outros) dos atuais alunos da UFSC.
A ordem correta sobre variáveis quantitativa ou qualitativa é:
A) qualitativa, quantitativa, qualitativa, quantitativa, quantitativa.
B) quantitativa, qualitativa, quantitativa, quantitativa, quantitativa.
C) qualitativa, quantitativa, qualitativa, quantitativa, quantitativa.
D) quantitativa, quantitativa, quantitativa, quantitativa, qualitativa.
117. (UFSC) Observe algumas variáveis de uma amostra de uma população a seguir:
1 – Idade
2 – Peso
3 – Cor dos olhos
4 – Sabor do sorvete
5 – Tipo de música ouvido com frequência
6 – Quantidade de vezes que foi ao teatro.
Sobre variáveis pode-se afirmar que
A) 1, 2 e 6 são variáveis quantitativas.
B) 2, 3 e 4 são variáveis qualitativas.
C) 4, 5 e 6 são variáveis quantitativas.
D) 1, 4 e 6 são variáveis qualitativas.
Veja mais projetos e planos: 💡
Plano de Aula: Jogo “Alvo dos Inteiros”
O Jogo “ALVO DOS INTEIROS“ é projetado para reforçar a compreensão dos alunos sobre inteiros e as quatro operações matemáticas básicas. Ao criar estrategicamente equações que alcançam ou se aproximam do número alvo, os alunos praticam o pensamento crítico e a resolução de problemas de uma maneira divertida e envolvente. Este tipo de jogo permite aos alunos visualizar e manipular conceitos abstratos de números inteiros em um contexto concreto, promovendo uma compreensão mais profunda e duradoura.
Link para o artigo, impressão e plano de aula (CLIQUE AQUI)






MATERIAL PERFEITO!
Parabéns pelas seleções das questões e criatividade em desenvolvê-las.